オブロングの箱（延長方形）

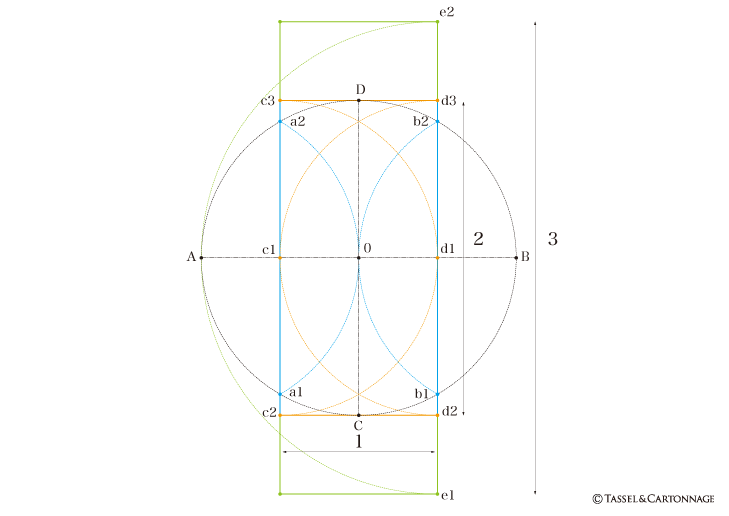
オブロングは「長方形の」という意味の四角形です。カルトナージュには形を形容した仏語読みの呼称があり、正方形はスクエア、長方形はレクタングル、引き伸ばされて細長い形や横に長い形をオブロング：延長方形と呼びます。

延長方形とは

延長方形は、長方形の中でも短辺と長辺の比を考える形ですが、図法よりも用い方を先に考えた捉え方をするのが実際だと思います。延長方形のプロポーションは、細く長い箱として短辺と長辺の差を開くため、少なくとも短辺１に対し長辺２以上に引き延ばした矩形が延長方形です。長辺が長くなるほどオブロングの形に見えてくるということです。

延長方形の図法

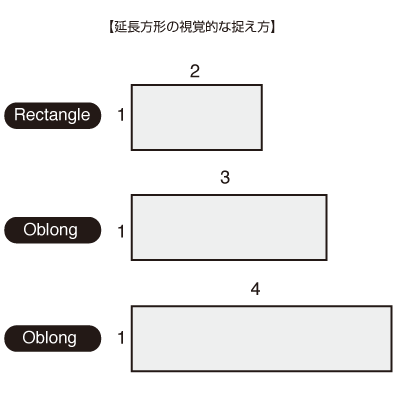
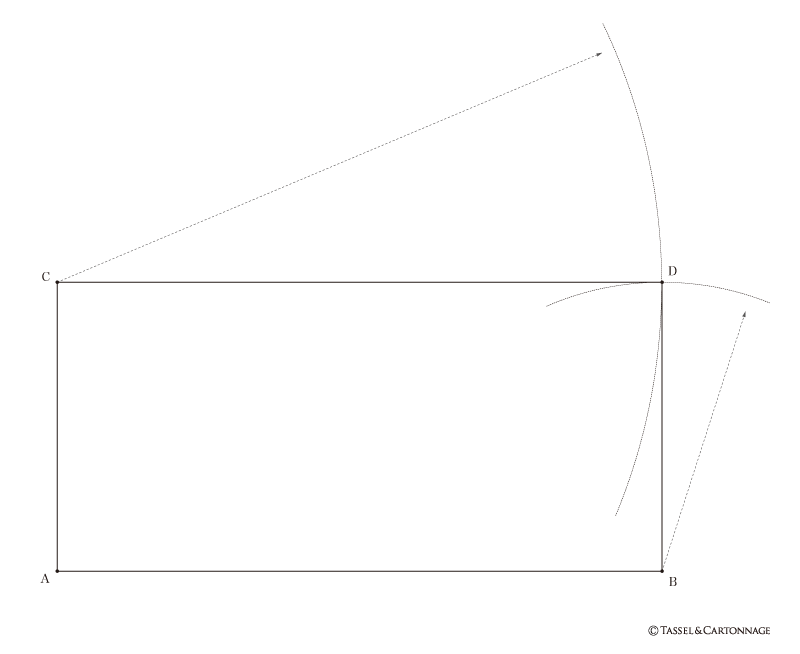
細長く横長の箱を作るための基本描画法は、三角定規を直角に組み合わせて長尺平行線を描画する方法が実際です。作図の基本である、直角、垂直線、平行線の描法です。仮に長方形（レクタングル）に近い場合は、下図に示す四角形の描き方を用いたりすることもあります。任意の長さの短辺と長辺を直角に結んで二辺を決めて、同じ長さ辺をコンパスで投影して求める基本図法です。延長方形の長尺平行線の描画は、互いに向き合う直線が平行であることと、直角で結ばれた矩形であることが重要なのです。

実際には、短辺と長辺の実長を元に平行描法で作図するほうが現実的でしょうが、次の製図法は、定正円を用いて延長方形の比率を定めるために策定した図法です。製図として応用したり、理解する上で知っておくとよい図法を示しておきます。定正円を元に短辺を１：長辺２の比率の定型図法ですが、１：３〜１：４と増やしていける作図の展開ができる図法です。